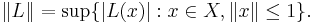Dual norm
The concept of a dual norm arises in functional analysis, a branch of mathematics.
Let X be a Banach space with norm  . Then the dual space X* is the collection of all continuous linear functionals from X into the base field (which is either R or C). If L is such a linear functional, then the dual norm of L is defined by
. Then the dual space X* is the collection of all continuous linear functionals from X into the base field (which is either R or C). If L is such a linear functional, then the dual norm of L is defined by
With this norm, the dual space is also a Banach space.
For example, if p, q ∈ 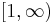 satisfy
satisfy 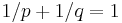 , then the ℓp and ℓq norms are dual to each other. In particular the Euclidean norm is self-dual (p=q=2). Similarly, the Schatten p-norm on matrices is dual to the Schatten q-norm.
, then the ℓp and ℓq norms are dual to each other. In particular the Euclidean norm is self-dual (p=q=2). Similarly, the Schatten p-norm on matrices is dual to the Schatten q-norm.